DISTRIBUSI NORMAL
Distribusi normal merupakan suatu alat statistik yang sangat penting untuk menaksir dan meramalkan peristiwa-peristiwa yang lebih luas. Distribusi normal disebut juga dengan distribusi Gauss untuk menghormati Gauss sebagai penemu persamaannya (1777-1855). Menurut pandangan ahli statistik, distribusi variabel pada populasi mengikuti distribusi normal.
Distribusi normal pertama kali diperkenalkan oleh Abraham DeMoivre (1733) sebagai pendekatan distribusi binomial untuk n besar. Selanjutnya dikembangkan oleh Pierre Simon de Laplace dan dikenal dengan Teorema Moivre - Laplace. Laplace menggunakan distribusi normal untuk analisis galat suatu eksperimen.
Distribusi normal merupakan salah satu distribusi probabilitas yang penting dalam analisis statistika. Distribusi ini memiliki parameter berupa mean dan simpangan baku. Distribusi normal dengan mean = 0 dan simpangan baku = 1 disebut dengan distribusi normal standar. Apabila digambarkan dalam grafik, kurva distribusi normal berbentuk seperti genta (bell-shaped) yang simetris.
Suatu data membentuk distribusi normal jika jumlah data di atas dan di bawah mean adalah sama.
Distribusi normal berupa kurva berbentuk lonceng setangkup yang melebar tak berhingga pada kedua arah positif dan negatifnya.
Ciri-ciri kurva normal :
- Bentuk kurva normal
- Menyerupai lonceng (genta/bel).
- Merupakan suatu poligon yang dilicinkan yang mana ordinat (sumbu tegak) merupakan frekuensi dan absisnya (sumbu alas) memuat nilai variabel.
- Simetris.
- Luas daerah merupakan nilai rata-rata (mean).
- Luas daerah sebelah kiri dan kanan mendekati 50%.
- Memiliki satu modus (disebut juga bimodal).
- Daerah kurva normal
- Merupakan ruangan yang dibatasi daerah kurva dengan absisnya (sumbu alas).
- Luas daerah biasanya dinyatakan dalam persen atau proporsi.
Distribusi normal dipengaruhi oleh dua parameter, yaitu mean dan standar deviasi.
Mean menentukan lokasi pusat statistik dan standar deviasi menentukan lebar dari kurva normal.
Rumus umum distribusi normal :
dengan
Kurva normal menggambarkan daerah penerimaan dan penolakan Ho.
Jika pengujian dua arah / sisi, maka gambarnya sebagai berikut :
Jika pengujian satu arah, maka gambarnya sebagai berikut :
Uji satu arah biasanya untuk uji F dan uji t satu arah.
Perhatikan kurva distribusi normal normal standar berikut:
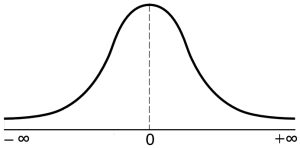
Sumbu X (horizontal) memiliki range (rentang) dari minus takhingga (‒∞) hingga positif takhingga (+∞). Kurva normal memiliki puncak pada X = 0. Perlu diketahui bahwa luas kurva normal adalah satu (sebagaimana konsep probabilitas). Dengan demikian, luas kurva normal pada sisi kiri = 0,5; demikian pula luas kurva normal pada sisi kanan = 0,5.
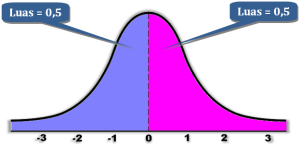
Dalam analisis statistika, seringkali kita menentukan probabilitas kumulatif yang dilambangkan dengan notasi P (X<x). Sebagai contoh, P (X<1), apabila diilustrasikan dengan grafik adalah luas kurva normal dari minus takhingga hingga X = 1.
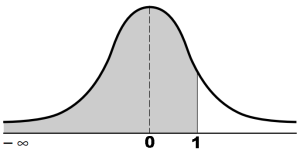
Secara matematis, probabilitas distribusi normal standar kumulatif dapat dihitung dengan menggunakan rumus:
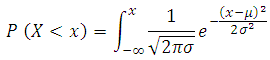
Akan tetapi, kita lebih mudah dengan bantuan tabel distribusi normal. Berikut adalah tabel distribusi normal standar, untuk P (X < x), atau dapat diilustrasikan dengan luas kurva normal standar dari X = minus takhingga sampai dengan X = x.
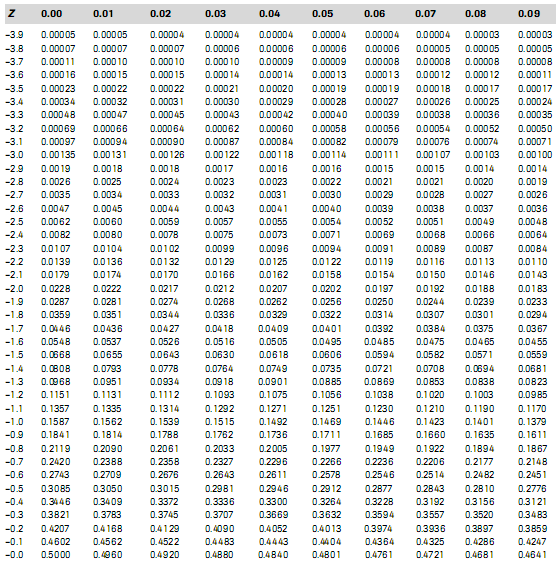
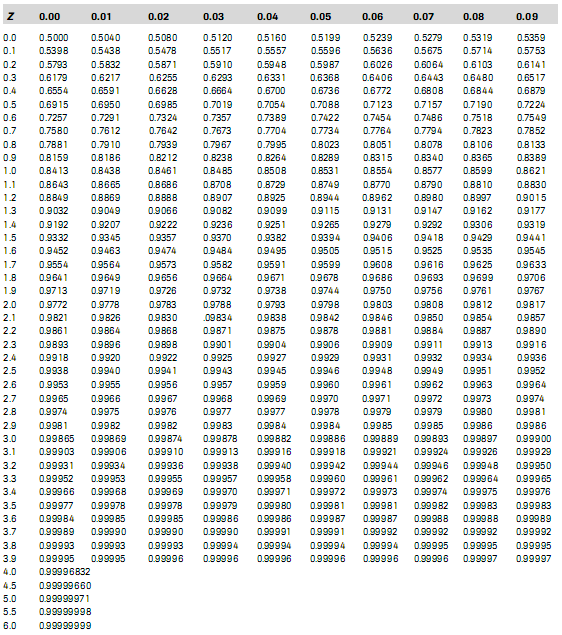
Contoh penggunaan:
Hitung P (X<1,25)
Penyelesaian: Pada tabel, carilah angka 1,2 pada kolom paling kiri. Selanjutnya, carilah angka 0,05 pada baris paling atas. Sel para pertemuan kolom dan baris tersebut adalah 0,8944.
Dengan demikian, P (X<1,25) adalah 0,8944.
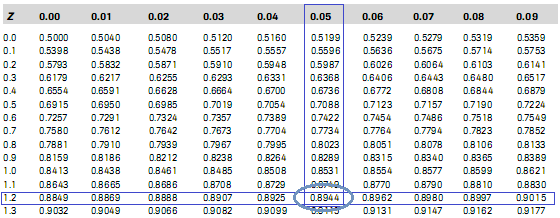
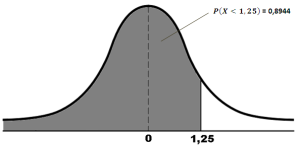
KURVA NORMAL
Kurva normal adalah satu model distribusi dari sejumlah kemungkinan distribusi. Hal ini diseb abkan karena penggunaan konsep kurva normal sangat luas dan dijadikan sebagai alat yang sangat penting dalam pengembangan suatu teori, konsep kurva normal juga memberikan status khusus dalam pengembangan kaidah-kaidah ilmiah.
Kurva normal bukan hanya satu kurva, melainkan mempunyai sejumlah kurva yang tidak terbatas yang mungkin dapat dibuat, dan semua itu dideskripsikan dengan suatu persamaan aljabar berikut.
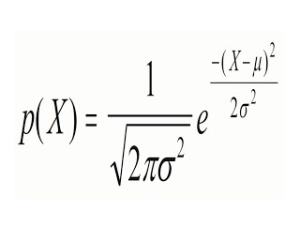
Persamaan di atas dapat membuat para pelajar menjadi panik dan/atau mengalami kesulitan untuk memahami konsep kurva normal. Secara umum, pemahaman atas persamaan aljabar ini tidak menjadi kebutuhan atau diperlukan untuk mengapresiasi dan menggunakan kurva normal. Namun demikian persamaan ini perlu dijelaskan untuk memahami bagaimana konsep dan aplikasi suatu kurva normal.
Pertama, penggunaan simbol-simbol dalam persamaan ini dimaksudkan untuk menyederhanakan proses perhitungan. Simbol-simbol itu termasuk “2″. “p”, dan “e”. Lambang “e” untuk menunjukkan adanya perhitungan dengan bilangan irasional atau untuk menunjukkan batasan yang sangat panjang. Hal ini dimungkinakn untuk menunjukkan “sejumlah keunikan”, dalam kasus “e” ini, yang menunjukkan “kekuatan khusus”
Kedua, adanya sekumpulan simbol yang menjadi kepedulian termasuk simbol “X”, yaitu melambangkan variabel responden untuk suatu skor nilai. Tinggi dari suatu kurva pada satu titik merupakan fungsi dari X (fx).
Ketiga, dua simbol terakhir dalam persamaan adalah “mu (μ) lambang darirata-rata ” dan “sigma (σ) lambang dari stadar deviasi” kedua lambang ini disebut dengan parameter atau nilai-nilai. Kedua parameter ini memberikan kemungkinan pembuatan kurva normal menjadi tidak terbatas, yaitu dengan menghubungkan kedua parameter ini. Dalam hal ini konsep parameter menjadi sangat penting dan perlu diperhatikan secara sungguh-sungguh.
Keluarga Distribusi
Kurva normal merupakan salah satu bentuk (anggota keluarga) dari sekian banyak (tidak terbatas) pola distribusi. Model setiap anggota keluarga ditentukan oleh seperangkat parameter (μ dan σ) dengan nilai (perhitungan) khusus. Sebab parameter σ dapat ditempatkan pada suatu nilai, posisitf atau negatif, dan parameter μ mempunyai nilai posisitf, hubungan dari kedua parameter ini membuat keluarga kurva normal menjadi luas sekali yang mempunyai anggota anggota tidak terbatas. Atas dasar itu, kurva normal diusulkan menjadi suatu model umum, karena asumsi kurva normal mampu menjelaskan sejumlah besar fenomena yang terjadi secara alami, mulai dari skor tes sampai ke fenomena bintang-bintang di langit.
Kesamaan Anggota Keluarga Kurva Normal
Anggota keluarga kurva normal sangat bervariasi mempunyai perbedaan, akan tetapi mempunyai sejumlah sifat-sifat umum yang sama, sifat-sifat umum ini disebut juga dengan kesamaan anggota keluarga kurva normal. Kesamaan (sifat-sifat umum ini) mencakup: bentuk simetri, mendekat ke ujung tetapi tidak pernah bersentuhan dengan sumbu X (asimtot), dan mempunyai wilayah di bawah kurva.
Dalam hal bentuk, semua anggota keluarga kurva normal mempunyai kesamaan yaitu berbentuk “lonceng”, kemudian sumbu X mempunyai kesamaan skala yang tepat. Sebagian besar wilayah di bawah kurva berada di sekitar titik tengan atau rata-rata. Ujung garis distribusi mendekat ke sumbu X tetapi tidak pernah menyentuh, dan luas wilayah di bawah kurvanya sangat kecil
Kesamaan dalam hal simetris, semua anggota keluarga kurva normal berada pada dua sisi sejajar dan simetris. Artinya, jika satu kurva normal digambarkan pada permukaan kertas dua dimensi, maka jika kertas itu dilipat pada garis tengahnya (garis rata-rata) maka kedua sisi kurva normal itu harus tepat sama. Keadaan simetris ini juga tergambar dalam struktur tubuh manusia, secara umum dalam posisi sejajar atau mendekati simetris antara sisi kiri dan kanan. Begitu juga dalam perkembangan kehidupan manusia baik individual maupun sosial.
Semua keluarga kurva normal mempunyai ekor mendekati sumbu X, tetapi tidak pernah menyentuhnya. Implikasinya, dibagian manapun suatu titik yang berada pada kurva (arah positif atau negatif) tetap saja mempunyai wilayah yang berada di bawah kurva normal. Oleh karena itu, gambar dari satu kurva normal harus mempunyai panjang garis yang tidak berhingga. Sehingga untuk mengeahui luas wilayah yang berada di bawah kurva normal harus dilihat dari suatu rentang yang dibatasi oleh sejumlah garis, hanya sebagaian kecil dari segmen garis yang digambarkan untuk kurva normal khusus.
Semua anggota keluarga kurva normal mempunyai total wilayah di bawah kurva sama dengan satu (1.00) , seperti yang terjadi pada model-model kemungkinan atau distribusi frekuensi. Sifat ini, menjadi tambahan pada sifat simetri, implikasinya bahwa wilayah pada setiap setengah dari distribusi adalah 0,50 atau setengah.
Sumber :




Tidak ada komentar:
Posting Komentar